The Gudermannian
In hyperbolic trigonomery, we come across the identity
\[\cosh^2 u = \sinh^2 u + 1.\]Recall that from classical trigonometry we also have
\[\sec^2 \phi = \tan^2 \phi + 1.\]They look curiously similar and is what would motivate the Gudermannian which seeks to connect classical trigonometry with hyperbolic trigonometry. In fact, the image of \(f(\phi) = (\sec \phi, \tan \phi)\) is also the hyperbola \(x^2-y^2=1\).
This motivates the following. Given any point on the right half of the unit circle, \((\cos \theta, \sin \theta)\), we could extend it to some point on the right branch of the hyperbola, \((\cosh u, \sinh u)\). This in turn gives us an angle \(\phi\) such that \((\sec \phi, \tan \phi) = (\cosh u, \sinh u)\).
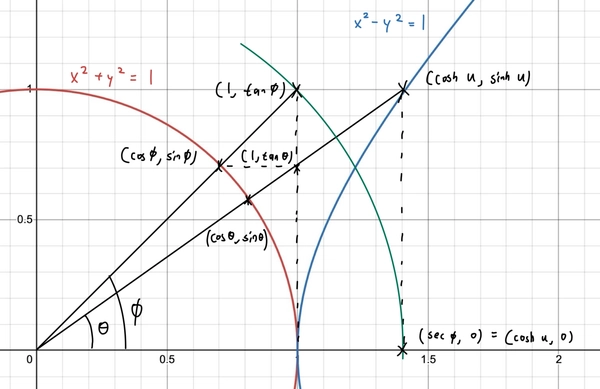
As such, we could relate \(u, \theta, \phi\) by
\[\tan \theta = \tanh u = \sin \phi.\]Derivatives
We could compute that
\[\begin{align*} \frac{du}{d\theta} &= \sec(2\theta), &\quad \frac{d\theta}{du} &= \text{sech}(2u).\\ \frac{du}{d\phi} &= \sec(\phi), &\quad \frac{d\phi}{du} &= \text{sech}(u).\\ \end{align*}\]which seems highly unobvious. We can show that \(\frac{du}{d\theta} = \sec(2\theta)\) geometrically. First consider the picture below.
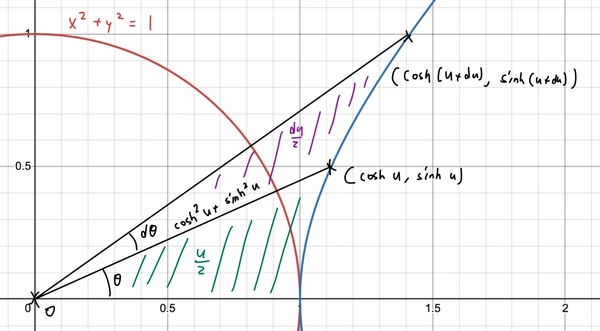
We have used the fact the the area of the hyperbolic sector is one half of the hyperbolic angle (similar to how the area of a circular sector in a unit circle is one half of the angle). Approximating the purple area \(du / 2\) with a circular sector of radius \(\cosh^2 u + \sinh^2 u\) and angle \(d\theta\), we get
\[\begin{align*} \frac{1}{2} \, du &\approx \frac{1}{2}(\cosh^2 u + \sinh^2 u) \, d\theta \\ &= \frac{1}{2}(\sec^2 \phi + \tan^2 \phi) \, d\theta \\ &= \frac{1}{2 \cos^2 \phi}(1 + \sin^2 \phi) \, d\theta \\ &= \frac{1}{2}\frac{1 + \tan^2 \theta}{1-\tan^2 \theta} \, d\theta \\ &= \frac{1}{2} \sec(2\theta) \, d\theta. \end{align*}\]Acknowledgements
Much of this post is inspired from an article by J. M. H. Peters.