Understanding the hyperbolic plane with refraction
We could think of the Poincaré’s half-plane model as a plane of transparent material with a specified refraction index. The light rays would correspond to geodesics.
This post is directly inspired by an article by Richard Montgomery
Classically the Poincaré’s half-plane model consideres the surface
\[\mathbb{H} = \{z \in \mathbb{C} \, \vert\, \text{Im } z > 0 \}\]endowed with the first fundamental form \(\frac{1}{y^2} (dx^2 + dy^2)\).
Alternatively we could think about the same upper half plane \(H:= \{(x,y) \in \mathbb{R}^2 \, \vert \, y > 0\}\) made with transparent material endowed with the refractive index
\[\eta(x,y) = \frac{1}{y}\]We could do so as the first fundamental form is a scaled version of the Euclidean metric \(dx^2 + dy^2\).
From this alone, we immediatedly expect vertical straight lines to still be geodesics (distances would not be shorted by deviating horizontally as the index is constant on horizontal lines) while lines pointing in other directions would curve.
To go further, we would need to appeal to Snell’s law which states that if a light ray crosses from an interface from a medium with index of refraction $\eta_1$ into a medium with index of refraction $\eta_2$, then the incident angle $\theta_1$ of the ray with the normal to the interface and the incident angle $\theta_2$ of the outgoing ray to that normal are related by
\[\eta_1 \sin \left(\theta_1\right)=\eta_2 \sin \left(\theta_2\right)\]In the continuum we would expect that \(\eta(t) \sin (\theta(t))\) to be kept constant throughout the geodesic, where \(\theta\) is the angle the light ray makes with the normal.
As such we have
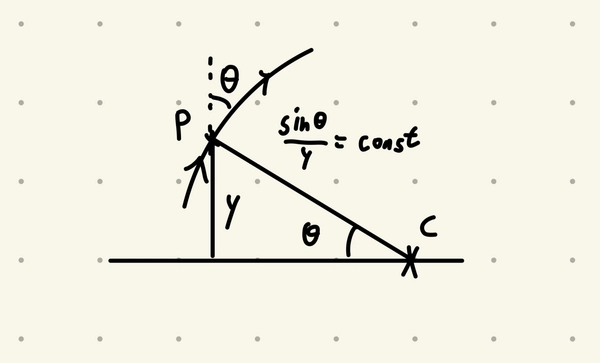
\[\eta \sin \theta = \frac{\sin \theta}{y} = \text{const}\]From the figure below, if a light ray has angle of incidence of \(\theta\) through some point \(P\), we see that it’s distance with some point \(C\) on the \(x\)-axis is kept constant i.e. the ray is the arc of a circle with center on the \(x\)-axis.
Going further
One may notice its similarities with mirages. Mirages form due to an increasing refractive index from hot air at the surface to the colder air above it. In our case, the refractive index decreases as \(y\) increases instead.
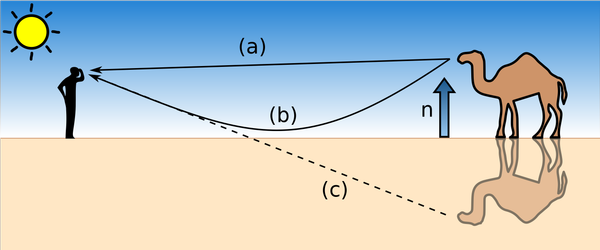
By MikeRun - Own work, CC BY-SA 4.0 Deed , Link
Acknowledgements
Apart from the aforementioned article by Richard Montgomery, I’m also inspired from a stack exchange answer from Jean Marie.