We take partial derivatives of the radius with respect to Cartesian coordinates all the time, especially in physics. While we can very easily do so with the quotient / chain rule, I’ve always been annoyed by that process (e.g. dealing with fractional exponents / cancelling out the 2s). As such, below is a proof by picture which is hopefully more illuminating / less frustrating.

Suppose we have the vector \(\mathbf{r}\) living in \(\mathbb{R}^2\) decomposed into its components \(\mathbf{r} = x \mathbf{e}_x + y \mathbf{e}_y\), where \(\mathbf{e}_x = (1,0)\) and \(\mathbf{e}_y = (0,1)\). Let’s define \(r = \sqrt{x^2 + y^2} = \|\mathbf{r}\|\), the length of \(\mathbf{r}\).

To find \(\partial_x r\), we shall compare the length of \(\mathbf{r}\) and \(\mathbf{r} + h \mathbf{e}_x\) for some small \(h\). We notice that as \(h \to 0\), we have \(\|\mathbf{r} + h \mathbf{e_x}\| \to r + h \partial_x(r)\). Taking this approximation., we can draw the following picture.

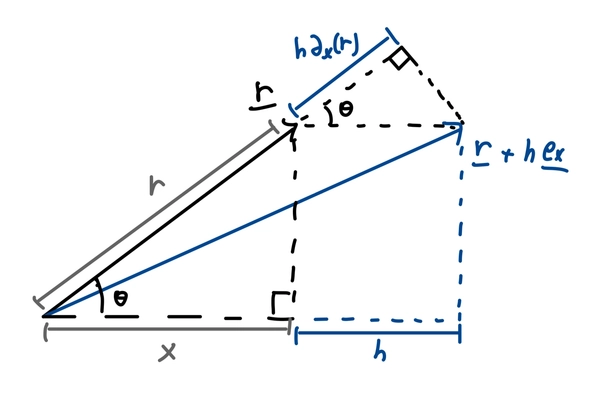
Focus on the two similar right triangles in the above picture that share the same angle \(\theta\), we have

\[\cos \theta = \frac{x}{r} = \frac{h\partial_x(r)}{h} = \partial_x(r).\]

Similarly, we can conclude

\[\sin \theta = \frac{y}{r} = \partial_y(r).\]

These results further inform us of the gradient of the radius.

\[\begin{align*} \nabla r &= \partial_x(r) \mathbf{e}_x + \partial_y(r) \mathbf{e}_y \\ &= \frac{x}{r} \mathbf{e}_x + \frac{y}{r} \mathbf{e}_y \\ &= \frac{\mathbf{r}}{r} \end{align*}\]

Algebraic method

We can also easily calculate that \(\nabla(x^2 + y^2) = 2 (x,y)\). So \(\nabla(r^2) = 2 \mathbf{r}\). Now by chain rule we also have \(\nabla(r^2) = 2r \nabla r\). Combining the two equations we get \(\nabla r = \mathbf{r}/r\).