Understanding Green's theorem
The statement of Green’s theorem is not particularly illustrative of the ideas driving it. We would try to gain some intuition by considering a simple example: finding the area bounded by a curve in the plane.
We would assume some knowledge of line integrals. Consider the following special case of Green’s theorem.
Theorem: Given some positively oriented, piecewise smooth, simple closed curve in a plane. Let D be the region bounded by C. Then the area of D is
\[\text{Area of }D = \iint_D dx dy = - \int_C y dx\]This looks awfully similar to finding the area under curves. Recall that
Lemma: Given a function \(y(x)\), the area under the curve \(\{(x, y(x)) \, | \, x \in [a,b]\}\) is \(\int_a^b y(x) dx\)
Can we use that idea alone to prove the theorem? Yes! Given some nice looking curve \(C\), we can split it into two parts. Express each part as some plot of some functions \(f(x), g(x)\).
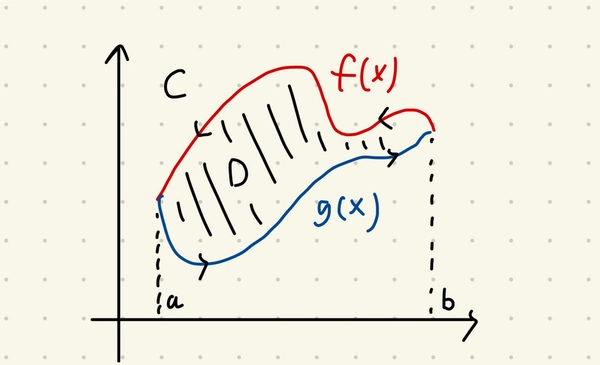
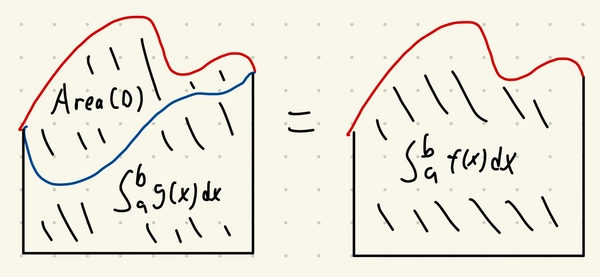
We could see that the area is now \(\int_a^b (f(x) - g(x)) dx\) which is the same as \(- \int_C y dx\)!
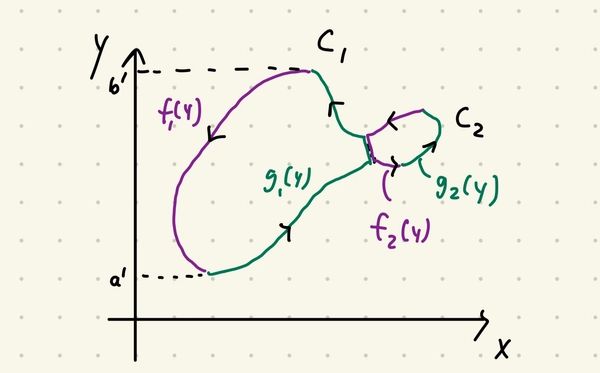
We could’ve done this by considering \(\int_C x dy\) instead. We would’ve had to taken a bit more care. In particular it would be nicer to split the curve into \(C_1\) and \(C_2\) so we get nice single-valued \(f_i(y)\) and \(g_i(y)\). (The reason we can split the curve is that the sum of the areas bounded by \(C_1\) and \(C_2\) is the area bounded by \(C_1\)) The driving principles are essentially the same.
Fundamentally, counting the area of a domain \(D\) should be a double integral \(\iint_D dx dy\). It’s only when we make some choice (and then using Green’s theorem or otherwise) would we have been able to reduce it into a single integral.
Generalisation
For the actual statement of Green’s theorem, one could refer to a lecture by MIT OpenCourseWare or a sketch of proof associated with the lecture (pdf).
Perhaps I would add an informal comment that a slight reformalisation of Green’s theorem would be
\[\int_C \bigg( \int M(x,y) dy \bigg) dx = \iint_D -M(x,y) dx dy\]which highlights the fact that in both sides of the equation two integrations had to be done: the number of integrations we do is the same. One may notice its similarities with Fubini’s theorem.
Here, we’ve made a choice of direction of integrating along the \(y\)-axis first, then the \(x\)-axis. We could’ve for example stated the following instead, which integrates along the \(x\)-axis first.
\[\int_C \bigg( \int N(x,y) dx \bigg) dy = \iint_D N(x,y) dx dy\]By rotating the plane the direction could be arbtiary. We could’ve even choosen to use other coordinates (such as polar coordinates).
The advantage of making a choice is that we could more easily relate the area integral with integrals over \(\mathbb{R}\). The disadvantage is that the formulation is less elegant / generalised than the Generalized Stokes theorem.