Let \(F(x)\) be a differentiable function. We’d like to show that

\[\int_a^b \bigg( \frac{d}{dx} F(x) \bigg)\,dx = F(b) - F(a)\]

Expanding the definition of the derivative and assuming we can swap limits and integrals, we would have

\[\begin{align*} &\int_a^b \bigg( \frac{d}{dx} F(x) \bigg)\,dx \\ &= \int_a^b \lim_{h \to 0} \frac{F(x+h) - F(x)}{h}\,dx\\ &= \lim_{h \to 0} \frac{1}{h} \bigg(\int_a^b F(x+h) \,dx - \int_a^b F(x) \,dx \bigg)\\ \end{align*}\]

For example with \(F(x) = \sin(x)\), \(a=0\), \(b=\pi/6\) and \(h=-0.1\), we would have \(\int_a^b F(x+h) \,dx - \int_a^b F(x) \,dx\) be the red shaded region below. The red curve is \(\sin x\) while the blue curve is \(\sin(x+h)\).

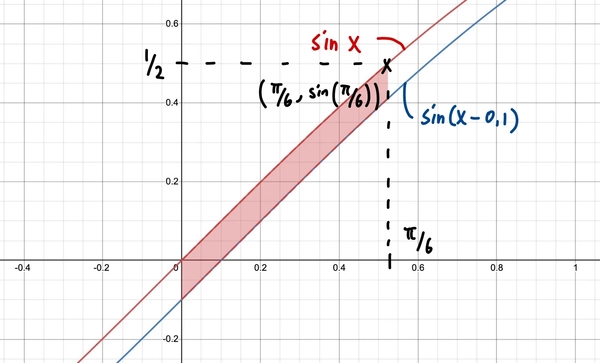
Notice that the red shaded region is very similar to the blue shaded region.

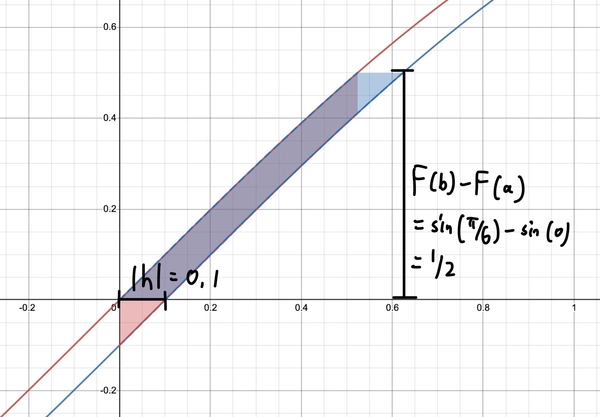
As \(h\) and \(b-a\) tends to 0, the blue shaded region looks more and more like a parellogram with height \(F(b) - F(a)\) and width \(h\) which has area \(h \times (F(b)- F(a))\) as such

\[\begin{align*} &\int_a^b \bigg( \frac{d}{dx} F(x) \bigg)\,dx \\ &= \lim_{h \to 0} \frac{1}{h} \bigg(\int_a^b F(x+h) \,dx - \int_a^b F(x) \,dx \bigg)\\ &= \lim_{h \to 0} \frac{1}{h} h \times (F(b) - F(a)) \\ &= F(b) - F(a) \end{align*}\]

Remarks

The advantage of this visualization is that we dealt with the differences of the area integrals more directly. The disadvantage is that we omitted using the intuition of the derivative / slope of \(F(x)\) all together.