Visualising composition series

I’ve found visualising composition series using curved exact sequences to be very helpful. The notation could be used to condese elementary theorems about solvable groups into a single picture. This post follows naturally from visualising the isomorphism theorems.

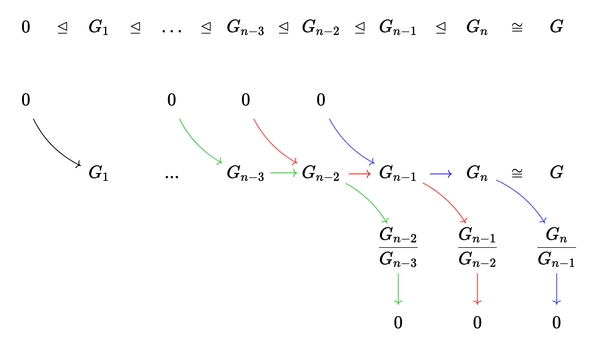
Composition series

The blue, red and green lines represent exact sequences. You could see that the fourth row are the composition factors.

Elementary theorems about solvable groups

You could find the full proofs of these in a standard group theory textbook.

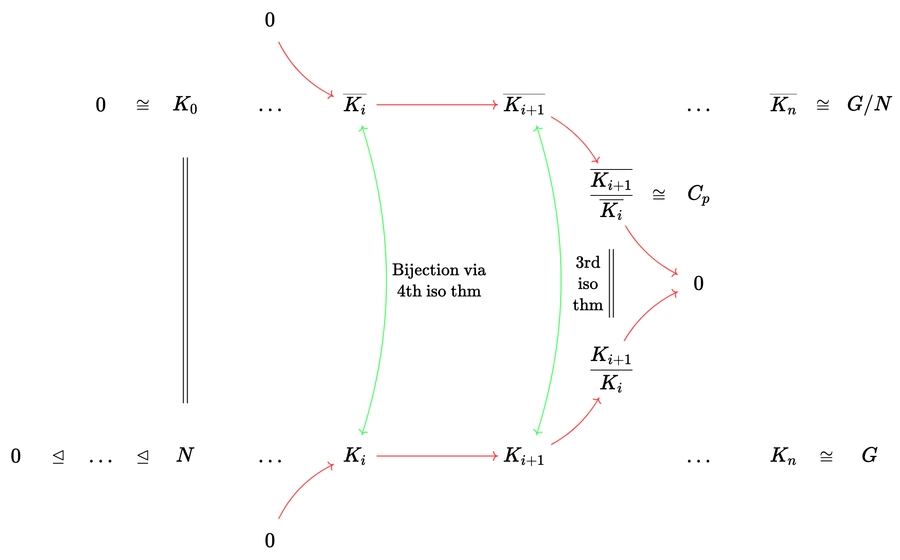
Theorem: If \(N\) normal subgroup of \(G\), and both \(G\) and \(G/N\) are solvable, then so is \(G\)

Proof: The idea is that the composition factors of \(G\) are those of \(N\) and \(G/N\) put together.

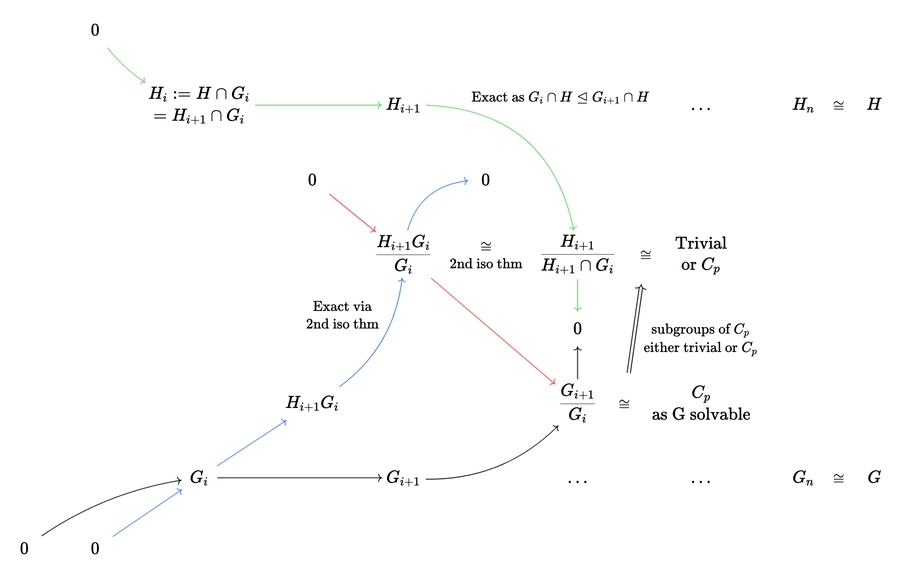
Theorem: If \(G\) is solvable, then any subgroup \(H\) of \(G\) is solvable

Proof: The idea is to let \(H_i = H \cap G_i\) where \(G_i\) is the composition series for \(G\).