Visualising the group isomorphism theorems

I’ve found the following diagrams to be very helpful at understanding and remembering the isomoprhism theorems. All the lines are represent exact sequences. The black lines represent the exact sequences introduced in the hypothesis, while the red lines represent the exact sequences introduced as conclusions. The equal sign in the graphs represents an isomorphism.

For abelian groups, Vakil’s visualisation is even neater. The picturebook already has visulasiations of the first and third isomorphism theorem so I would draw my own interpertation for the second and fourth isomorphism theorem.

First isomorphism theorem

Statement: Let \(\phi: G \to H\) be a group homomorphism. Let \(\ker \phi\) be the kernel of \(\phi\). Then \(\text{Im } \phi \cong G / \ker \phi\)

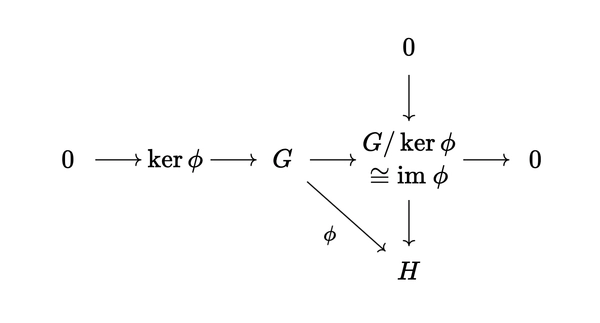
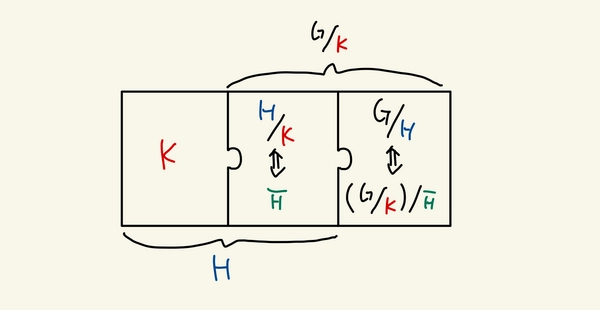
Second isomorphism theorem

Statement: Let \(G\) be a group. Let \(N \trianglelefteq G\) and \(H \leq G\). Then

\[\dfrac{H}{H \cap N} \cong \dfrac{HN}{N}\]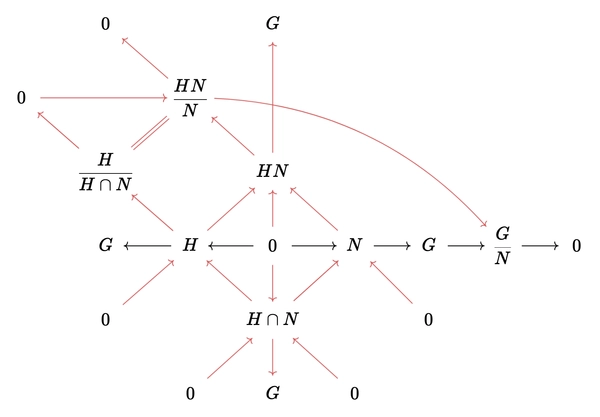

In accordance with Vakil’s notation. Supposing that \(G\) is abelian (so that all subgroups are normal), we would have

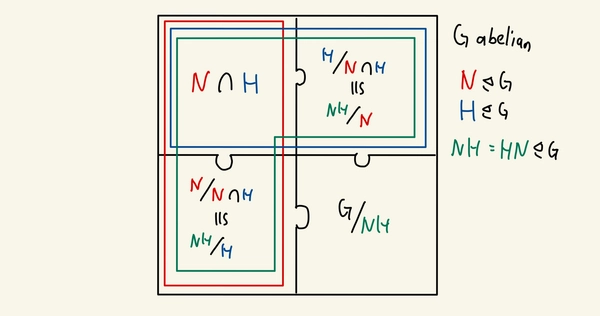
Third isomoprhism theorem

Statement: Let \(G\) be a group. Let \(N \trianglelefteq G\), \(K \trianglelefteq G\) and \(K \leq N\). Then \(K \trianglelefteq N\) and

\[\dfrac{G/K}{N/K} \cong \dfrac{G}{N}\]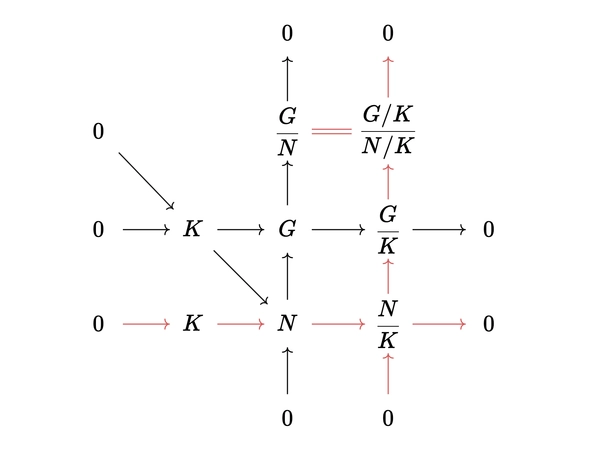

Fourth isomorphism theorem

The full statement can be found here. In short,

Statement: If \(G\) is a group and \(K \trianglelefteq G\). Then there is a bijective map from subgroups of \(G\) containing \(K\) to subgroups of \(G / K\).

The graph below approximates the statement. In that the red exact sequences correspond to the blue exact sequences.

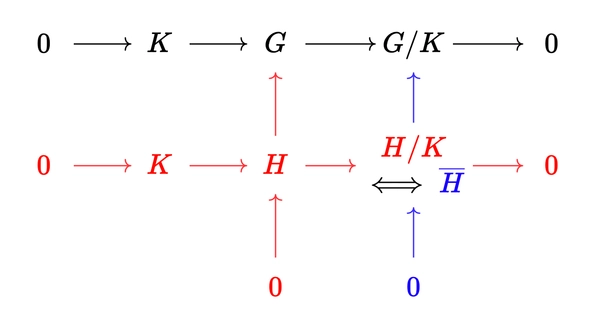
In accordance with Vakil’s notation. Supposing that \(G\) is abelian (so that all subgroups are normal and abelian), we would have

Further Remarks

The definition of a semi-natural product fits naturally inside the graph for the second isomorphism theorem.

We could also go further and visualize the composition series.

Next maths post Previous maths post

All maths posts