Understanding the Jordan Normal Form
We aim to understand the strategy of the proof of Jordan Normal Form theorem through analyzing a very simple example of a nilpotent matrix. It’s intended for readers who have already read a bit about the Jordan Normal Form and would like to get a higher level overview.
Introduction
The Jordan Normal Form is one of the many normal forms in mathematics. Normal Forms gives you a standard way of expressing a mathematical object up to some equivalence relation / classification. In particular the Jordan Normal Form aims to express all square matrices in an algebrically closed field up to similarity.
The proof of Jordan Normal Form theorem is long wided. Personally, I think the most interesting feature of the JNF is the series of 1 and 0s along the off-diagonal. Why that feature shows up can be boiled down to proving the following theorem.
Let \(V\) be finite dimensional. Let \(T: V \to V\) be a linear transformation. If \(T^n = 0\) for some \(n > 0\) then \(T\) is called nilpotent.
Theorem: If \(T\) is nilpotent, then its minimal polynomial has the form \(m_T(x) = x^m\) for some \(m\) and there exists a basis \(B\) of \(V\) such that:
\[_B[T]_B = \begin{bmatrix} 0 & * & & 0\\ & \ddots & \ddots & \\ & & \ddots & * \\ 0 & & & 0 \end{bmatrix}\]where each \(*\) is \(0\) or \(1\)
Let’s assume that this theorem is true, construct an example of a nilpotent transformation using the form provided by the theorem, and understand how that transformation acts on \(V\). Hopefully that would give us an idea of how to prove the theorem!
Example
Let \(V = \mathbb{F}^8\) and \(T\) has the following matrix with respect to the standard basis.
\[\begin{bmatrix} 0 & 1 & 0 \\ & 0 & 1 & & & \smash{\text{\LARGE 0}}\\ & & 0 \\ & & & 0 & 1 \\ & & & & 0 \\ & & & & & 0 & 1 \\ & &\smash{\text{\LARGE 0}} & & & & 0 \\ & & & & & & & 0 \\ \end{bmatrix}\]The first thing you could think of is perhaps to seperate it into Jordan blocks. We’d get 1 3-block, 2 2-blocks and 1 1-blocks. It’s clear that \(T^n\) would ahnilate all the blocks with dimension less than equal to \(n\). So we need \(n\) to be at least 3 to ahnilate the 3-block. Hence the minimal polynomial is intuitively \(m_T(\lambda)=\lambda^3\). It’s also clear the characteristic polynomial \(\chi_T(\lambda)\) would be \(\lambda^8\) to match the dimensions of the matrix.
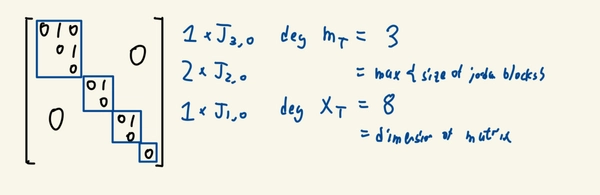
We can also look into the kernels of \(T^n\) for various \(n\). It’s clear that \(\ker T^3 = V\). But what about \(\ker T^2\) and \(\ker T\)?
Looking at the matrix, clearly the 1st column vector is in \(\ker T\). We also see that \(T\) maps the 2nd column vector to the 1st column vector and the 3rd to the 2nd. So the 2nd column vector is in \(\ker T^2\) and the 3rd column vector is in \(\ker T^3\). Intuitively, we are able to find a basis of the kernels from the column vectors alone (without considering their linear combinations).
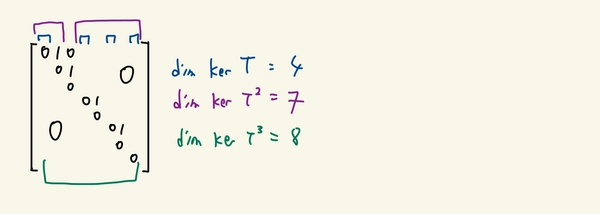
We could also name the column vectors smartly. For each Jordan block, we only need to name the rightmost vector. The rest of the column vectors in that block can be expressed as \(T^k\) acting on that vector.
This gives us an interesting way to describe a basis for the kernels.
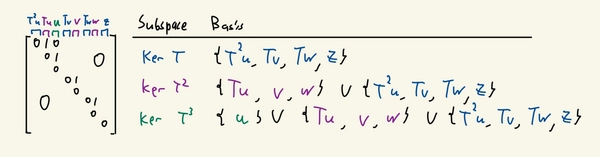
In particular if we are using the terminology of quotient spaces, it seems like there’s a recursive element to these bases. Notice how \(B_n\) is an extension of \(T(B_{n+1})\).
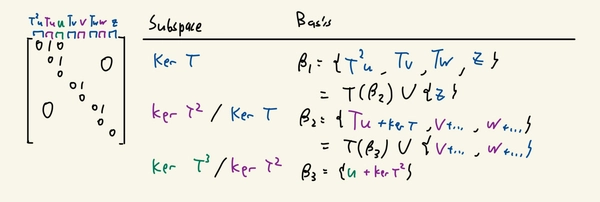
This suggests that for an arbtiary nilpotent matrix of index \(m\), we start by considering \(\ker T^m / \ker T^{m-1}\) and move downwards, carrying over basis vectors by applying \(T\) and picking up additional basis elements along the way.
Treating it as a game
Let’s work over a \(n\)-dimensional vector space \(V\). Suppose \(T: V \to V\) is nilpotent with index \(m\)
Another way of thinking about it is that we want to find an ordered set \(S = \{v_1, \dots ,v_n\}\) that’s a basis and also has the property \(Tv_i = v_{i-1}\) or \(0\) for all \(i\)
If we only needed \(S\) to be spanning it’s not difficult. Choose any basis \(\{u_1, \dots u_n\}\). For every \(u_i\) there exists a minimal \(m_i\) such that \(T^{m_i} u_i = 0\). So we construct the set \(\{T^{m_1 - 1}u_1, \dots ,u_1, T^{m_2-1}u_2, \dots ,u_n\}\) and it’s clearly spanning and has the property we want.
To reduce the size of this set (in hopes of finding a minimal generating set / a basis), it’s clear we need to pick vectors wisely. When we pick the first vector, we should pick the vector \(v\) with the maximum minimal \(m\) such that \(T^m v = 0\). Otherwise it’s possible that we would end up picking some vector \(u\) down the road such that \(Tu = v\) and so we would get duplicate vectors. This idea suggests we should consider \(\ker T^m / \ker T^{m-1}\) first.
It’s also clear that one of the difficulties of the proof is justifying linear independence.
A lot of these ideas appear in a formal proof which one can find here.