Sequences sometimes extend to good examples of smooth functions with special properties e.g. interesting limsups and liminfs. For example, you may want construct a smooth function \(h(x)\) that continuously alternates between \(f(x)=x\) and \(g(x)=0\) so that it has a limsup of infinity and liminf of 0. By observation we could choose \(h(x)=\vert x \sin x\vert\). We would try to generalise this.

Remark: While we could use bump functions to produce a similar effect, it feels somewhat more elegant to use trignometric functions instead.

Definitions

We call a sequence \((a_n)\) \(k\)-periodic for some positive integer \(k\) if there exists smooth functions \(f_i : \mathbb{R} \to \mathbb{R}\) for \(i \in \{0, 1, \dots , k-1\}\) such that \(a_n = f_i (n) \text{ if } n \equiv i \; (\text{mod } k)\)

For example, \(a_n = (-1)^n\) is 2-periodic with \(f_0(x) = 1, f_1(x) = -1\).

2-periodic sequences

Proposition: If \((a_n)\) is 2-periodic, then there exists a smooth function \(f: \mathbb{R} \to \mathbb{R}\) such that for all \(n \in \mathbb{N}\), \(f(n) = a_n\)

Proof: Suppose \((a_n)\) 2-periodic with associated \(f_0\) and \(f_1\) functions. Let

\[f(x) = \cos^2 \bigg(\frac{\pi x}{2}\bigg) f_0(x) + \sin^2 \bigg(\frac{\pi x}{2}\bigg) f_1(x)\]

We could see that if \(x\) is an even integer then \(f(x)=f_0(x)\) and if \(x\) is an odd integer then \(f(x) = f_1(x)\). Clearly \(f\) smooth as trignometric functions, \(f_0\) and \(f_1\) are smooth.

\[\blacksquare\]

For example, we can extend \(a_n=(-1)^n\) to \(f(x) = \cos^2 (\frac{x \pi}{2}) - \sin^2 (\frac{x \pi}{2}) = \cos (\pi x)\).

k-periodic sequences

Proposition: If \((a_n)\) is k-periodic, then there exists a smooth function \(f: \mathbb{R} \to \mathbb{R}\) such that for all \(n \in \mathbb{N}\), \(f(n) = a_n\)

Proof: Suppose \((a_n)\) k-periodic with associated \(f_0, \dots , f_{k-1}\) functions. Let

\[g_j(x) = \sin \bigg(\frac{\pi}{k} (x-j) \bigg)\]

for \(j \in \{0, 1, \dots k - 1\}\)

Note that for all \(j \in \{0, 1, \dots k - 1\}\) and integers \(i\), we have \(i \equiv j \; (\text{mod } k) \iff g_j(i) = 0\). Now we consider

\[f(x) = \sum_{i=0}^{k-1} \bigg[ \bigg(\prod_{j=0, j \neq i}^k \frac{g_j(x)}{g_j(i)} \bigg) f_i(x) \bigg]\]

We can the verify that \(f\) is smooth and satisfies \(f(n) = a_n \; \forall n \in \mathbb{N}\). The idea is that each of the \(g_j\) acts a sieve and annihilates the necessary terms.

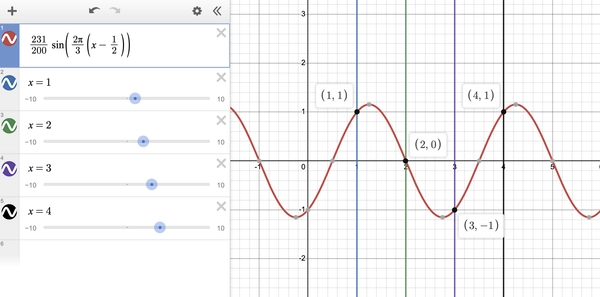
\[\blacksquare\]

For example we can extend the sequence \(-1, 1, 0, -1, 1, 0, -1, \dots\) (assuming the sequence starts at \(0\)) which is 3-periodic with \(f_0(x) = -1, f_1(x) = 1, f_2(x) = 0\) into

\[\begin{align*} f(x) &= -\frac{\sin(\frac{\pi}{3}(x-1)) \sin(\frac{\pi}{3}(x-2)) }{\sin(\frac{\pi}{3}(0-1)) \sin(\frac{\pi}{3}(0-2))} \\ &\phantom{=}+\frac{\sin(\frac{\pi}{3}(x-0)) \sin(\frac{\pi}{3}(x-2)) }{\sin(\frac{\pi}{3}(1-0)) \sin(\frac{\pi}{3}(1-2))} \\ &= \frac{231}{200} \sin\bigg( \frac{2\pi}{3} (x- \frac{1}{2})\bigg) \end{align*}\]

Here’s a graph of the function,