Interiors, closures and boundaries of topological spaces
I’d show alternate definitions of interiors, closures and boundaries for topological spaces which I’ve found immensely helpful.
Let’s go through the usual definitions first. Given a topological space \(X\) with a subset \(S \subset X\), the interior \(\text{int}(S)\) of \(S\) is defined to be the union of all open subsets of \(X\) that is contained in \(S\). The closure \(\overline{S}\) is defined to be the intersection of all closed subsets of \(X\) containing \(S\). \(\overline{S} \backslash \text{int}(S)\) is known as the boundary of \(S\) and denoted \(\delta S\).
The equivalent definitions I like to use are
\[\begin{align*} a \in \text{Clo}(S) \iff& \nexists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset X \backslash S,\\ a \in \text{Int}(S) \iff& \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset S,\\ a \in \delta S \iff&\nexists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset S \\ &\text{ and } \nexists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset X \backslash S. \end{align*}\]The similarities in the definitions prompts us to define the following. Given some \(a \in X\) we let \(P\) and \(Q\) be the statements
\[\begin{align*} P &: \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset S,\\ Q &: \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset X \backslash S. \end{align*}\]It’s impossible for \(P\) and \(Q\) to both be true so we have the truth table
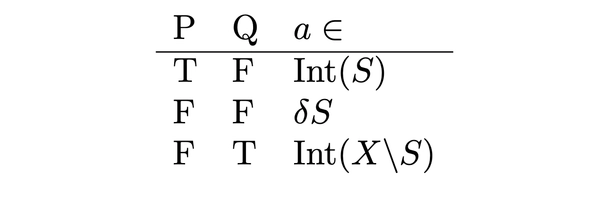
This means \(\text{Int}(S)\), \(\delta S\) and \(\text{Int}(X \backslash S)\) partition \(X\)
Accumulation and isolated points
Let \(S'\) denote the set of accumulation points of \(S\) and \(\text{Iso}(S)\) denote the set of isolated points of \(S\), we have the equivalent definitions
\[\begin{align*} a \in S' &\iff \nexists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \backslash \{a\} \subset X \backslash S, \\ a \in \text{Iso}(S) &\iff \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \backslash \{a\} \subset X \backslash S\text{ and } a \in S. \\ \end{align*}\]This shows that we’re concerned with \(U \backslash \{a\}\) for open sets \(U\) that contain \(a\). Inspired by how we defined \(P\) and \(Q\), we define the following statements \(V\), \(W\) and \(K\) for some \(a \in X\) as follows.
\[\begin{align*} P &: \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset S,\\ Q &: \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \subset X \backslash S, \\ V&: \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \backslash \{a\} \subset S, \\ W&: \exists \text{ open } U \subset X \text{ s.t. } a \in U \text{ and } U \backslash \{a\} \subset X \backslash S, \\ K&: a \in S. \end{align*}\]Using this language, we can see the following equivalences.
\[\begin{align*} a \in S' &\iff \neg W, \\ a \in \text{Iso}(S) &\iff W \land K. \end{align*}\]Also note that
\[\begin{align*} P &\iff V \land K, \\ Q &\iff W \land \neg K. \end{align*}\]As such \(\neg Q \iff \neg W \lor K \iff (\neg W) \text{ XOR } (W \land K)\). So accumulation points and isolated points form a partition of the closure.
We can further split into cases. Considering the interior of \(S\) first, notice that \(P \land \neg Q \iff V \land K\). So we have the following cases
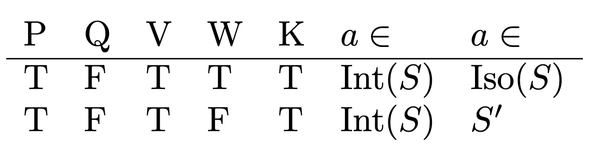
Considering the boundary \(\delta S\), we also have \(\neg P \land \neg Q \iff (K \land \neg V) \lor (\neg K \land \neg W)\). So we have
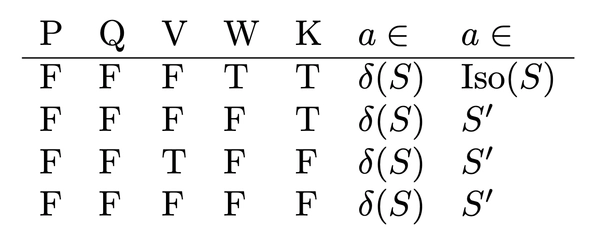
We can conduct a similar analysis for the interior of \(X \backslash S\).
Examples
Consider the real line with the topology induced from the Euclidean metric. Let \(S=((0,2] \cup \{3\})\backslash\{1\}\). Then we have

Note that \(\text{Int}(S) \cap \text{Iso}(S) = \emptyset\) for all subsets \(S\) of \(\mathbb{R}\). However if we consider some discrete topological space \(X\), then \(\text{Int}(S) \cap \text{Iso}(S) = S\) for all subsets \(S\) of \(X\).