To show that the open disc without the origin is homotopy equivalent to the circle, one could imagine having a circle with radius \(1/2\) centred at the origin with uniform mass inside the disc.

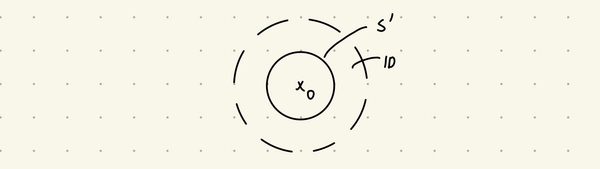
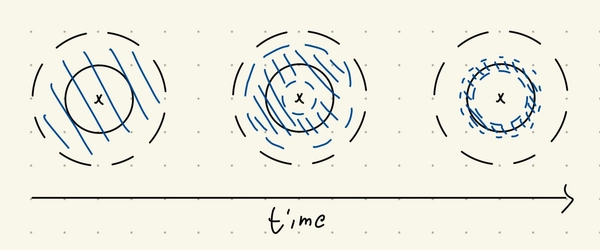
If we then consider the gravitational field due to the circle, we can see that it’s nonzero for all points except the origin. Following the vector field, it’s clear that with zero initial velocity, every point in the disc except the origin is going to end up at some point in the circle. There’s an issue in that there’s no upper bound to the time to which the points end up in the circle. I’m not sure how that could be resolved, perhaps by magnifying the field strength such that it is either 0 or \(\geq c\) for some small constant \(c\) across the disc.

Where the point ends up at would be how we define the homotopy retract. We could then use the (altered) gravitational flow to construct our show that the homotopy retract composed with the inclusion map is homotopic to the identity.

This argument works for more complicated examples. For example, to show that the wedge sum of two circles, \(S^1 \wedge S^1\), is homotopy equivalent to the open disc with two points removed, one could imagine embedding \(S^1 \wedge S^1\) inside the disc and giving it uniform mass.

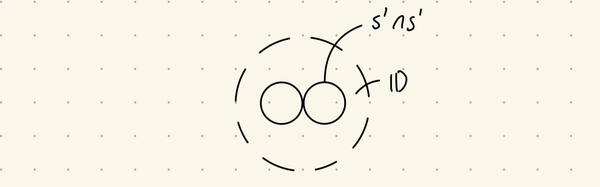
By symmetry, there should be three points in the disc where the gravitational field is zero. Excluding all three points except the origin, we would recover the open disc with two points removed. We could then construct the homotopy retract similarly.

Contractability

We may also gain some intuition to the contractability of spaces using gravity. For example to show that the open disc is contractible, one could imagine putting a point mass in the origin which pulls everything in the disc towards it in finite time.

However for a circle, no matter where you put the point mass, the opposite point would always have gravitational field zero. This is clearly not a proof that a circle is not contracible but it does give some sort of intuition.