Introduction to symmetries and its applications

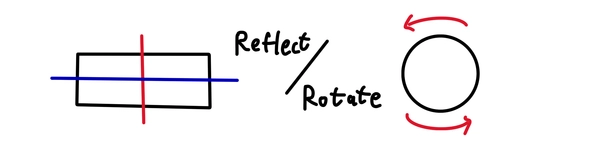
Speaking of symmetries, you may think of the rotational symmetries of a circle or the reflection symmetry of a rectangle. It turns out that symmetries like these greatly help us in simplifying, solving and understanding physical problems in the real world.

Starting from rotational symmetry, we can generalise the idea of symmetries. There are two components to every symmetry: An action changes the object from one perspective (a circle is rotated around its centre), yet the object stays the same from another perspective (it looks like it has the same shape). Under this generalisation, what other symmetries are there?

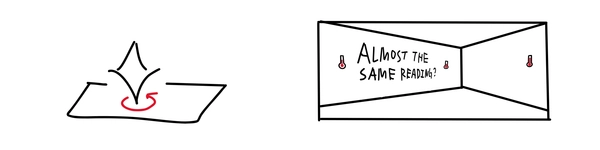
One example is the passing of time. If there’s an aspect of an object that stays the same as time passes, we say that the object exhibits a time symmetry. For example, imagine a spinning top on a desk. In an ideal world without friction, how fast the top spins remains the same whenever you measure it. As such, we say that the top’s spinning velocity exhibits a time symmetry.

Another example is changes in space. Many physical properties may be invariant under spatial changes. For example, the temperature in a room is almost the same wherever you place the thermometer (unless you place it near a heater!) The position changes, yet the temperature measured remains (roughly) the same. We call this spatial symmetry.

The abstract study of these symmetries is very much of interest to pure mathematicians, but as you would see they are also very useful in modelling real life and solving problems.

Pretend you’d like to know how far a cannon shoots out a cannonball. One way to do it is to model the cannonball flying through the air to figure out its path. Ignoring air resistance might give you too bad of a prediction, but considering the atomic interactions between the cannonball itself would be excessive.

As such, by making appropriate assumptions about the problem at the cost of realism, we’d increase the likelihood of getting a model that’s feasibly computable. A lot of these assumptions often come in the form of symmetries.

Going back to the cannonball, we could assume that the cannonball is spherical and the airflow around it is cylindrically symmetric. We could also assume that the gravitational force on the cannonball is the same regardless of how high it is. (i.e. we assume gravitational force is invariant under spatial transformations, even though gravity decreases the higher up you get)

In general, mathematical modelling is very much an art of balancing simplicity and realism. By choosing the right details to focus on and discarding the others, we’d extract the essence of the problem at hand in a timely fashion.

As we go down the atomic scale, more and more complicated symmetries exist in the subatomic particles and the forces between them, which require more and more mathematics to describe fully.

These symmetries, and their exploitations, shape much of the quantum physics we know today.

Remarks

This was written to apply for an internship in Tom Rocks Maths. Thought I’d share it here.

I’ve been inspired by this wikipedia article on symmetries in physics. The discussion on mathematical modelling is also very much inspired by a talk given by Derek Moulton for the Invariants.

I’ve also been inspired by a very recent post on symmetries in string theory by Dewi Gould, a postgrad student at Oxford.