HKDSE Physics and M2 (Part III)
In the final post of this series, we would discuss waves. How do we formulate waves mathematically? Why are waves often depicted by sine curves?
Wave equation
The wave equation is the (partial differential) equation that describes all sorts of waves (water, sound, light …) It can be written compactly as
\[\ddot u = c^2 \nabla^2 u\]Unfortunately, to understand and derive the above would involve heavy calculus, even if we confine ourselves to one-dimensional waves. If you’re interested in the derivation of the one-dimensional wave equations, you could look at chapter 4 of this set of lecture notes.
Instead, we would like to explore the mathematical formulation of the sinusoidal travelling wave. The sinusoidal travelling wave is one of many solutions to the wave equation and is the one studied extensively in DSE physics.
The one-dimensional sinusoidal travelling wave could be represented by
\[u(t,x) = A \sin (kx - wt + \psi)\]where \(x\) is distance and \(t\) is time for some constants \(A, k, w, \psi\). Try guessing what physical meaning those constants have! It would be revealed at the end of the post.
You could imagine this as a function from \(\mathbb{R}^2\) to \(\mathbb{R}\). It takes in time and distance and tells you the displacement of the wave.
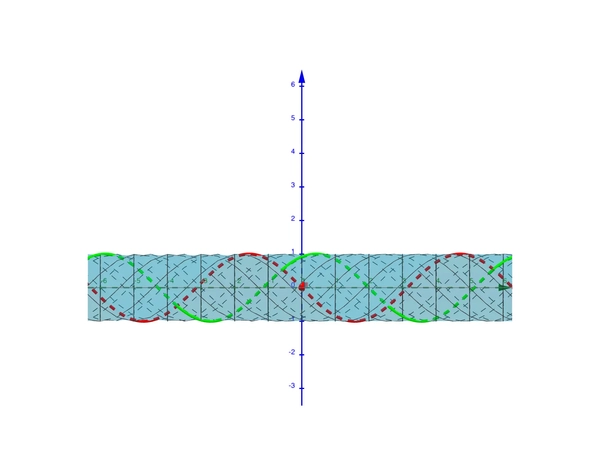
In the graph below, we took \(A=w = k = 1\) and \(\psi = 0\). The x-axis is red and the t-axis is green.
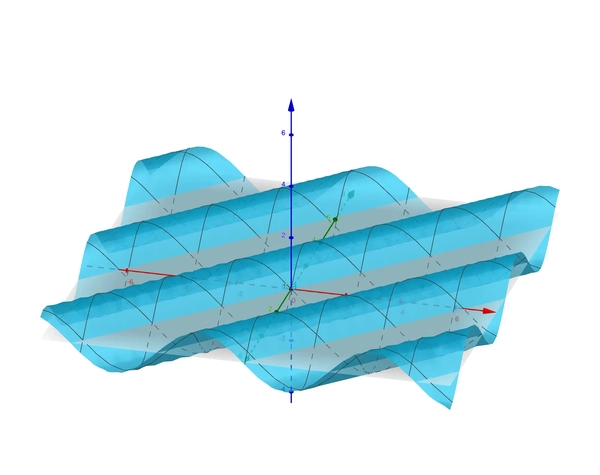
We can look at how the wave looks like at time \(c\) by considering the intersection of the graph \(u(t,x)\) and the plane \(t=c\).
In the graph below, we took \(t=0\) for the red curve and \(t=2\) for the green curve.
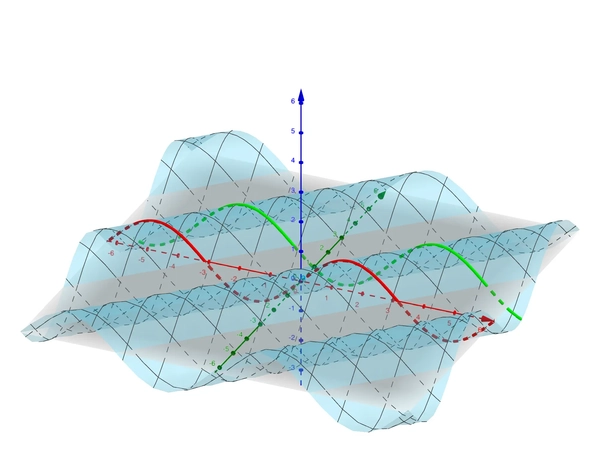
If we look at the graph along the time axis, does this look like displacement time graphs? Can you guess what direction the wave is travelling to? How could we change the direction of the wave? What is the wavelength? How does the wavelength correspond to the constants?
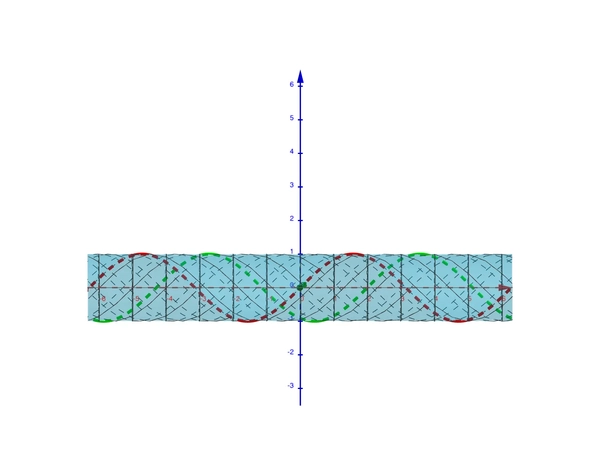
Similarly, if we’re interested at a particular distance \(x=c\), we could look at the intersection of the graph \(u(t,x)\) and the plane \(x=c\).
In the graph below, we took \(x=0\) for the red curve and \(x=2\) for the green curve.
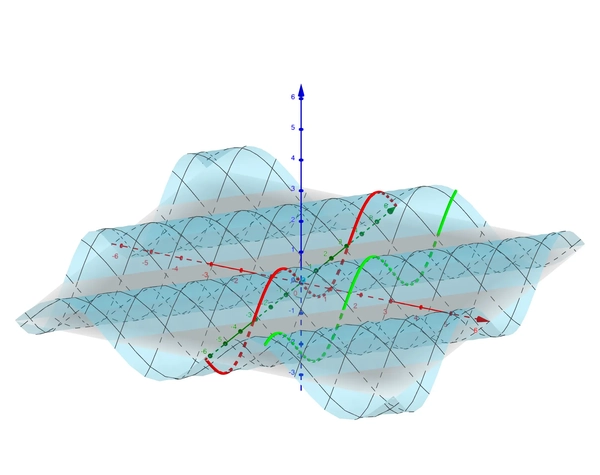
If we look at the graph along the distance axis, does this look like displacement distance graphs? What is the period of the wave? How does the period correspond to the constants?
Answers and more questions
Turns out, the wavelength \(\lambda\) is equal to \(1/k\) and \(w\) is the (angular) frequency of the wave. Can you deduce why that is the case?
What about \(\psi\)? What does it represent?
Can you think of how to parametrize stationary waves using a similar \(u(x,t)\)?
Further Reading
For more on one-dimensional wave equations, you could look at this LibreTexts article.