There’s a lot of examples of pointwise but not uniform convergence. But I suppose it wouldn’t harm to have another one. The following is certainly not original.

Motivation

Imagine a wave packet that travels horizontally from the origin to infinity with a velocity of \(1\). Let \(f_t(x)\) be a snapshot of that wave at time \(t\)

It’s clear that as time progresses, the wave packet would eventually pass through all points in \(\mathbb{R}^+\).

Focusing on one point \(x_0\), once the wave passes through it completely, the amplitude on that point would be \(0\) from then on.

However for all time \(t\), there’s always a point on \(\mathbb{R}^+\) such that the amplitude is nonzero.

Construction

Let \(f_t(x)\) be a sequence of functions from \(\mathbb{R}\) to \(\mathbb{R}\).

\[f_t(x) := \left\{ \begin{array}{ll} x-(t-1) & \text{if } t-1 \leq x \leq t \\ -(x-(t+1)) & \text{if } t < x \leq t+1 \\ 0 & \text{otherwise} \end{array} \right.\]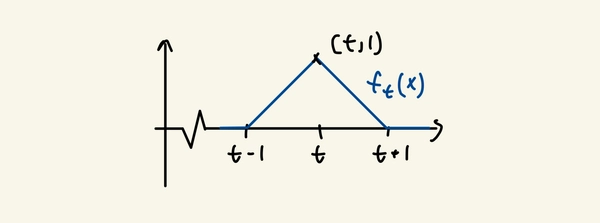

Graph of ft(x)

Clearly \(f_t(x)\) is continuos on \(\mathbb{R}\).

Let \(x_0\) be some real number. If \(t > x_0 + 1\), then \(f_t(x_0) = 0\). So \(\lim_{t \to \infty} f_t(x_0) = 0\) and hence \((f_t(x))\) is pointwise convergent to \(0\).

However, \(f_t(t) = 1\) for all \(t \in \mathbb{R}\), so \(\lim_{t \to \infty} \sup \{\lvert f_t(x) - f(x) \rvert : x \in \mathbb{R}\} = 1 \neq 0\) and hence \((f_t(x))\) does not uniformly converge to \(0\).

Fatou’s Lemma

It’s also a nice function to demonstrate Fatou’s lemma. We can observe

\[0 = \int \liminf_{t\to \infty} f_t(x) \leq \liminf_{t\to \infty} \int f_t(x) = 1\]

Further Reading

There’s a lot of great examples in this website as well.